To celebrate what in the US we call 3.14 or PI day, today I’m offering stories that deal with mathematics and circles. First up, an app named for the great philosopher who is credited – even if perhaps ahistorically so – with finding that ratio and ratios in harmonies.
Technology has long introduced innovations that make playing easier for specialists and non-specialists alike. Just ask anyone who plays an instrument like the guitar – frets, and the simplified notation that went with it, go back centuries as a means of allowing more people to make music.
Developer Rob Fielding wants to rethink frets, to bring their disposition and playability closer to the way harmonics work in sound. The creator of the microtonal iPad app Mugician, his next app in development, Pythagoras, offers some fascinating ideas. Forgive me getting a bit theoretical in the prose for those who do speak that language; the videos are always the best way of understanding what’s going on. (The vast majority of even untrained ears have the ability to perceive pitch with astounding accuracy, so you don’t have to be an expert. Usually when people claim to be tone deaf, the problem is that they can’t sing, not that they can’t hear, in my experience.)
I’ll let Rob explain:
Pitch
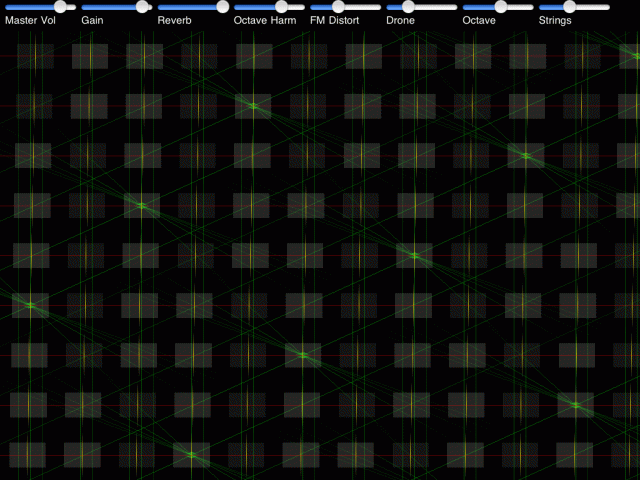
Pythagoras’ fretless mode uses geometry to mark the harmonically relevant points, not fixed frets. Where the lines intersect with strings, the notes are perfect ratios to each other. This helps you to locate and get to know the useful pitches that are used in world music. [See image, top for a beautiful visualization of how this works. -Ed.] That is explained here:
The Spectrum – Pythagoras’s interfaceWhen you play a chord like a major third, you line up the blue notes to overlap perfectly, and you get shiningly perfect major thirds that way. Same for harmonically correct fifths and fourths. These are the pitches that you hear as overtones when you listen carefully to instruments with lots of sympathetics, etc.
I do want to respond to this one lamentation in Rob’s post: he frets (ahem) that MIDI doesn’t use frequency, and that OSC isn’t well-supported. I actually think MIDI isn’t far off – it just lacks precision. Perception of pitch is complex, but a logarithmic scale (in which 440 sounds one octave higher than 220) is reasonably close to how we hear. And that’s precisely what MIDI gives you; if you just wanted to number the piano, its solution of using a number like 60 for middle C makes perfect sense. (We can overlook for a moment that the definition of MIDI fumbled the octave. The basic idea was still right.)
Even outside MIDI, a numbering system like that in MIDI – mapping pitch space to a logarithmic scale to make them match intuitively what we hear – is not uncommon. The problem is that MIDI doesn’t have a rational way of dealing with what happens in between the notes, as it used integers for efficiency. Take MIDI’s logarithmic scale and set floating-point numbers (numbers with a decimal place, like 60.5 instead of 60), and you have a pretty decent solution. You could still, if you didn’t want integers to represent 12-tone equal-tempered pitch, apply different scales and modes. But I think if you wanted a decent way of communicating note values, unless I’m really missing something, sending floating point numbers that default to a 12-TET logarithmic scale can’t be too bad. I understand that most instruments don’t yet respond in any standardized way, but I refuse to believe this is an intractable problem. I’m happy to discuss in comments. Heck, if we just got Max and Pd patchers to agree on something, I’d be pleased.
On to another very cool idea:
Octave Rounding
Pythagoras is using octave rounding in its latest incarnation when you press the “Auto” button for the octave switch. What this means is simply that it doesn’t care about what octave a note is in, it will pick the closest octave to the last played note. This allows for astounding feats of arpeggiation and pentatonic scales – even when playing fretless. Here is the more popular video:
And here is the improvement upon it the next day (much less viewed video) where you can slide up or down a fourth:
This octave rounding is an idea I implemented a few years ago in my Samchillian derivative called Xstrument. (Both Xstrument and Mugician are open source projects on github). This idea is very applicable to 2 octave keyboards as well.
Here is the idea with a trivial Pd program:
It’s really great stuff. As it happens, I’ve been exploring new geometries for music making myself, interested along similar lines. And musical inventor Roger Linn has had a lot of things to say about it lately, too, including his respect for Rob’s work.
So, I’d love to have a discussion. What interesting interfaces have you seen for music? Are there any you find playable in practical circumstances? And why can’t we just solve this issue of how to transmit pitch information between software and hardware once and for all? (I don’t yet know how HD-MIDI will address the issue; that’ll be interesting to see.)
And don’t miss Rob’s blog:
http://rrr00bb.blogspot.com/
Finally, here’s Jordan Rudess rocking out with Mugician, Rob’s (currently-available) app.